回溯与迷宫
回溯与迷宫

46排列组合1

题目

Given a collection of distinct integers, return all possible permutations.

Example:

1
2
3
4
5
6
7
8
9
10
Input: [1,2,3]
Output:
[
  [1,2,3],
  [1,3,2],
  [2,1,3],
  [2,3,1],
  [3,1,2],
  [3,2,1]
]

分析

这道题目的很明确，就是要求出数组所有排列组合情况，重点是不重复的数字，也就是说我们并不用考虑重复排列的情况

代码1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public List<List<Integer>> permute(int[] nums) {
   List<List<Integer>> list = new ArrayList<>();
   // Arrays.sort(nums); // not necessary
   backtrack(list, new ArrayList<>(), nums);
   return list;
}

private void backtrack(List<List<Integer>> list, List<Integer> tempList, int [] nums){
   if(tempList.size() == nums.length){
      list.add(new ArrayList<>(tempList));
   } else{
      for(int i = 0; i < nums.length; i++){
         if(tempList.contains(nums[i])) continue; // element already exists, skip
         tempList.add(nums[i]);
         backtrack(list, tempList, nums);
         tempList.remove(tempList.size() - 1);
      }
   }
}

47排列组合2

问题

Given a collection of numbers that might contain duplicates, return all possible unique permutations.

Example:

1
2
3
4
5
6
7
Input: [1,1,2]
Output:
[
  [1,1,2],
  [1,2,1],
  [2,1,1]
]

代码2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public List<List<Integer>> permuteUnique(int[] nums) {
    List<List<Integer>> list = new ArrayList<>();
    Arrays.sort(nums);
    backtrack(list, new ArrayList<>(), nums, new boolean[nums.length]);
    return list;
}

private void backtrack(List<List<Integer>> list, List<Integer> tempList, int [] nums, boolean [] used){
    if(tempList.size() == nums.length){
        list.add(new ArrayList<>(tempList));
    } else{
        for(int i = 0; i < nums.length; i++){
            if(used[i] || i > 0 && nums[i] == nums[i-1] && !used[i - 1]) continue;
            used[i] = true;
            tempList.add(nums[i]);
            backtrack(list, tempList, nums, used);
            used[i] = false;
            tempList.remove(tempList.size() - 1);
        }
    }
}

回溯算法

步骤

用回溯算法解决问题的一般步骤：

  1. 针对所给问题，定义问题的解空间，它至少包含问题的一个（最优）解。
  2. 确定易于搜索的解空间结构,使得能用回溯法方便地搜索整个解空间 。
  3. 以深度优先的方式搜索解空间，并且在搜索过程中用剪枝函数避免无效搜索。

基本思想

回溯算法的基本思想是：从一条路往前走，能进则进，不能进则退回来，换一条路再试。比如走迷宫问题，就是这条路走不通，然后返回前一个路口，继续下一条路。回溯算法说白了就是穷举法。不过回溯算法使用剪枝函数，剪去一些不可能到达 最终状态（即答案状态）的节点，从而减少状态空间树节点的生成。

回溯与动态规划

这道题让我想起之前的爬楼问题，都是一个问题由一个或者几个子问题构成，不断划分
他们之间的区别在于：动态规划往往是寻找一个最优解，而回溯问题则是穷举，深度遍历所有情况，当然也存在不符合要求的情况，但是仍然要遍历到相应的节点上。

适用情况

  • 穷举问题，例如在某个范围内求所有可能情况
  • 搜索空间均可以表示成树的样子

用回溯思想解决问题

回到问题

排列组合1

首先，我们来看，这是一种不需要剪枝的问题，得到的所有解一定唯一，那我们看一看程序是怎么实现回溯的：

图示: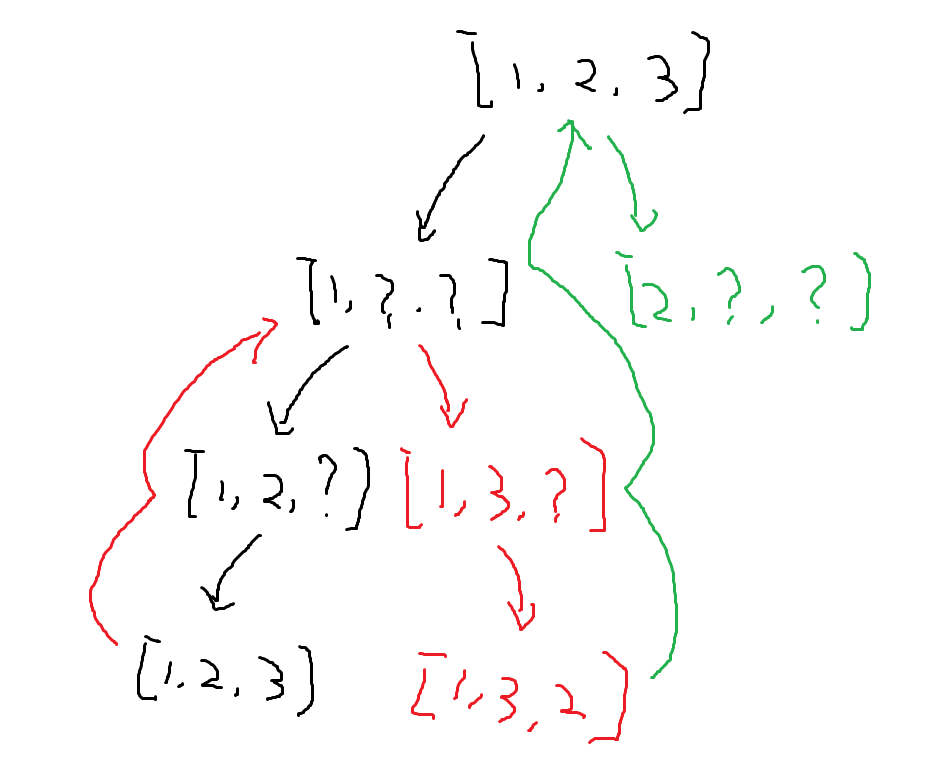

回溯算法
回溯算法

  1. 首先明确回溯是一个递归性质的问题，这道题模型是传一个待排列数组和原数组。
  2. 从0位置依次加入待排列数组，由于每次递归都要从0位置开始判断，所以传入之后要先判断这个数组是否已经出现过这个位置上的数，如果不曾出现，把这个数加入到数组中，再次递归。
  3. 直到依照这个方法将数组填满(tempList.size() == nums.length)，把这样计算出来的数组加入到结果中。这样其中的一个分枝就完成了。
  4. 完成之后自然进行回溯(跳出该层递归)，寻找下个排列组合。

排列组合2

这个问题和上面区别不是很大，首先关键点是先用sort函数将数组排序，使重复的元素都放在一起，下面主要说一下剪枝判断的设计
首先，用used[i]布尔型数组来判断是否该元素是否已经被排列组合过。
判断语句if(used[i] || i > 0 && nums[i] == nums[i-1] && !used[i - 1])

  1. 前一个used[i]相当与问题1中的判断，即当前待排列数组中是否包含了其本身（这种情况并不是重复，而是其本身）；
  2. 后面i > 0 && nums[i] == nums[i-1] && !used[i - 1])其实想表明的意思是该元素与前面的元素重复，并且等于这个值的元素已被排列好；

这两种情况便可跳过排列组合，也就是剪枝

注意的问题

1
tempList.remove(tempList.size() - 1);

注意这个语句，由于我们待排列数组只有一个，我们不断更新，加入的标志是已满，如果得到第一种满足条件的情况直接返回，那么这个排列数组一直保持满的状态，不在会被更新，所以回溯的时候要注意，把带排列数组元素-1，才能有新排列组合情况进来。
其他问题也同样，如果维持的是同一个数据结构，注意回溯的时候回退数据结构中的内容。

总结

讲了那么多，我们需要注意回溯的几个关键要素

  1. 迭代
    回溯问题体现在程序设计上大多数是递归，而每一层递归又会有一个循环来遍历这层递归的所有情况
  2. 条件
    对于每个特定的解的某一步，他必然要符合某个解要求符合的条件，如果不符合条件，就要回溯，其实回溯也就是递归调用的返回。
  3. 结束
    当到达一个特定结束条件时候，就认为这个一步步构建的解是符合要求的解了。把解存下来或者打印出来。对于这一步来说，有时候也可以另外写一个issolution函数来进行判断。注意，当到达第三步后，有时候还需要构建一个数据结构，把符合要求的解存起来，便于当得到所有解后，把解空间输出来。这个数据结构必须是全局的，作为参数之一传递给递归函数。而且要注意：如果维持的是同一个数据结构，注意回溯的时候回退数据结构中的内容。

后面几天我会多找一些关于回溯算法的题来品尝。

更多关于回溯的问题

更多关于回溯算法的问题请转到回溯算法标签