Leetcode日记：51&52.N皇后问题

题目

The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens attack each other.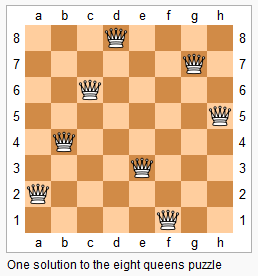

八皇后问题的一个解法
八皇后问题的一个解法

Given an integer n, return all distinct solutions to the n-queens puzzle.

Each solution contains a distinct board configuration of the n-queens’ placement, where ‘Q’ and ‘.’ both indicate a queen and an empty space respectively.

Example:

1
2
3
4
5
6
7
8
9
10
11
12
13
Input: 4
Output: [
 [".Q..",  // Solution 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // Solution 2
  "Q...",
  "...Q",
  ".Q.."]
]
Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above.

题目分析

这就是这次回溯问题的最终难题————经典的八皇后问题，题目主要的要求就是在摆N个皇后之后，皇后之间不能相互碰到。
这也要求我们利用回溯思想解决问题，当然不用回溯也是可以的，但是回溯的精妙之处在于其简洁，明了。让我们看看代码是如何实现的吧。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Solution {
    List<List<String>> result = new ArrayList<>();
    public List<List<String>> solveNQueens(int n) {
        boolean[] visited = new boolean[n];
        //2*n-1个斜对角线
        boolean[] dia1 = new boolean[2*n-1];
        boolean[] dia2 = new boolean[2*n-1];
        
        fun(n, new ArrayList<String>(),visited,dia1,dia2,0);
        
        return result;
    }
    
    private void fun(int n,List<String> list,boolean[] visited,boolean[] dia1,boolean[] dia2,int rowIndex){
        if(rowIndex == n){
            result.add(new ArrayList<String>(list));
            return;
        }
        
        for(int i=0;i<n;i++){
            //这一行、正对角线、反对角线都不能再放了，如果发现是true，停止本次循环
            if(visited[i] || dia1[rowIndex+i] || dia2[rowIndex-i+n-1])
                continue;
            
            //init一个长度为n的一维数组，里面初始化为'.'
            char[] charArray = new char[n];
            Arrays.fill(charArray,'.');
            
            charArray[i] = 'Q';
            String stringArray = new String(charArray);
            list.add(stringArray);
            visited[i] = true;
            dia1[rowIndex+i] = true;
            dia2[rowIndex-i+n-1] = true;

            fun(n,list,visited,dia1,dia2,rowIndex+1);

            //reset 不影响回溯的下个目标
            list.remove(list.size()-1);
            charArray[i] = '.';
            visited[i] = false;
            dia1[rowIndex+i] = false;
            dia2[rowIndex-i+n-1] = false;
        }
    }
    
}

代码分析

回溯思想

这道题的回溯思想和之前我们两道题基本一致，并没有过于难的地方：

结构：：

  • 递归（迭代）：这道题本身就是DFS问题，首先从第一行第一个开始，试着放一个皇后，接下来把相关信息放入，继续迭代(层数加一，rowIndex+1)，当发现满足条件时存入数组并返回。
  • 条件：当放入的皇后数量等于目标数便可存入，当无解后会自动结束。在每一次布局时，共同维护着三个Boolean数组，来判断是否皇后会打架。（详细见下文）
  • 结束：当一次迭代执行完毕之后，不管这个方法成功与否，都把当前得到的排布的最后一行删掉list.remove(list.size()-1)，并初始化这一行，并且还原Boolean数组，重新安排这一行的下一种布局（回溯）。

关于打架的判断

上文提到，每一次布局都会有与之对应的三个Boolean数组，这个数组便是检测在这一列、副对角线，主对角线上的皇后是否产生打架，这个规则不容易想，首先，我们以数组的形式来模拟棋盘：

1
2
3
4
5
[0,0][0,1][0,2][0,3][0,4]
[1,0][1,1][1,2][1,3][1,4]
[2,0][2,1][2,2][2,3][2,4]
[3,0][3,1][3,2][3,3][3,4]
[4,0][4,1][4,2][4,3][4,4]

我们来找一下：
visited[i] 是与之对应的列，这个很显然。
dia1[rowIndex+i]说的是副对角线，可以观察到副对角线上，行（rowIndex）与列（i）之和是一样的。
dia2[rowIndex-i+n-1]说的是副对角线，仔细观察发现主对角线上，行（rowIndex）与列（i）之差是一样的，但是为了避免出现数组索引为负数的情况，代码特意在后面+n-1。

关于回溯时的状态重置

回溯状态重置这个问题已经是老生常谈了，但是仍然要引起重视，这是很容易遗漏的一点。

首先，回溯之前，要把之前迭代的不符合要求或者已经存入的上一层内容清空重置（谨记只是上一层内容），反映到此题上就是

1
2
list.remove(list.size()-1);
charArray[i] = '.';

相比之前几道题已经讲过很多次了。

还有就是要把判断状态表重置，反映在此题就是

1
2
3
visited[i] = false;
dia1[rowIndex+i] = false;
dia2[rowIndex-i+n-1] = false;

52题简要说明

这道题比第一个简单很多，只要求输出有多少种摆法。只需要在原看来代码的基础上删去不必要的List<List<String>> result，然后添加一个int型变量，得到满足条件的结果就+1就可以了。

更多回溯算法

更多关于回溯算法的问题请转到回溯算法标签