这篇文章基本来自《码出高效》这本书, 由我自己总结归纳一些基础性的知识。
部分图和源代码来自于CarpenterLee博客
从最简单的树说起
1.树(Tree)
相对来说,树是一个很基础的概念, 不需要去多谈。
需要掌握两个概念:
深度:从根节点出发,到某节点边的条数。
高度:从某结点出发,到叶子节点为止, 最长简单路径上边的条数。
2.平衡二叉树
高度差为 1 的二叉树。
其性质如下:
(1)树的左右高度差不能超过 1
(2)任何往下递归的左子树和右子树, 必须符合第一条性质。
(3)没有任何节点的空树或只有根节点的树也是平衡二叉树。
3.二叉查找树(又名二叉搜索树,Binary Search Tree)
性质:对于任意节点,它的左子树上所有节点的值都小于他, 而他的右子树上的所有节点的值都大于他。
遍历节点的三种方式:前序遍历、中序遍历、后序遍历。**他们三者规律如下**
(1)在任何递归子树中, 左节点一定在右节点之前遍历。
(2)前序、中序、后序,仅指根节点在遍历时的位置顺序。
AVL 树与树形旋转
AVL是一种平衡二叉查找树, 增加或删除节点后通过树形旋转重新达到平衡。
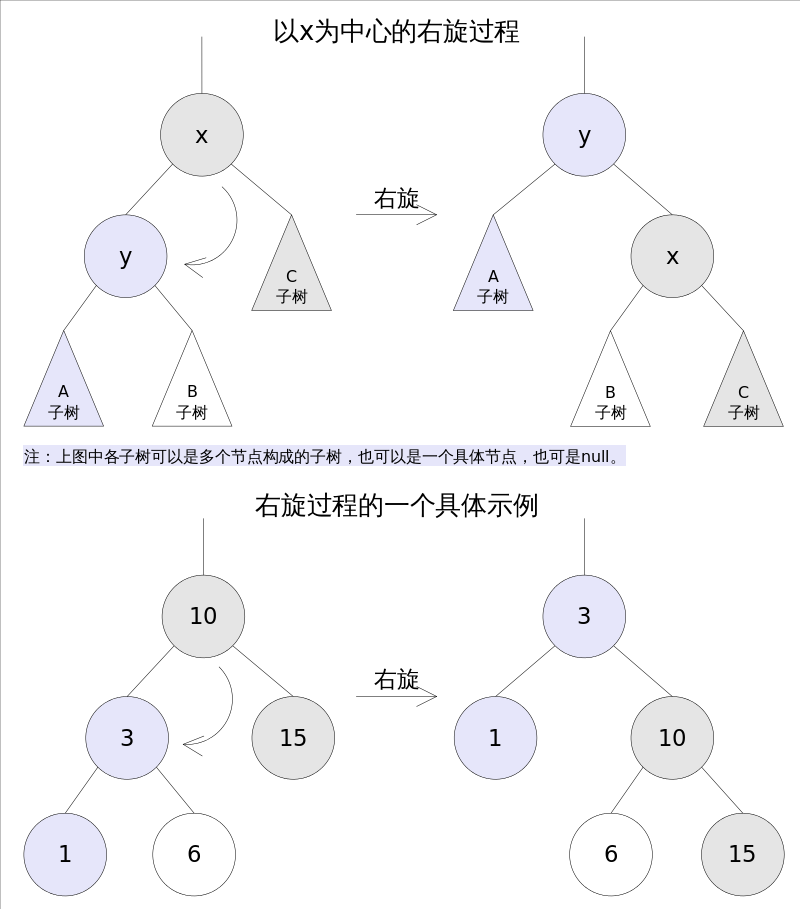
右旋:以某个节点为中心, 将他沉入当前右子节点的位置, 而让他当前的左子节点作为新树的根节点,也称为顺时针旋转;
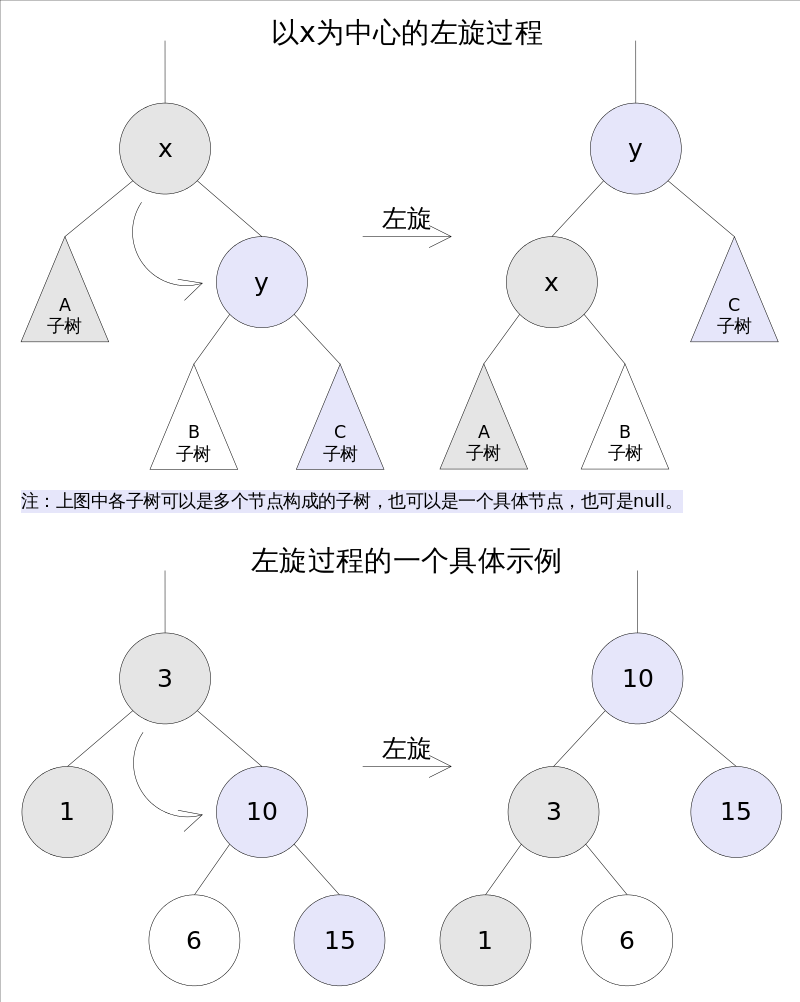
左旋:以某个节点为中心, 将他沉入当前左子节点的位置, 而让他当前的右子节点作为新树的根节点,也称为逆时针旋转;
左旋图示
右旋图示
左旋源代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
private void rotateRight(Entry<K,V> p) {
if (p != null) {
Entry<K,V> l = p.left;
p.left = l.right;
if (l.right != null) l.right.parent = p;
l.parent = p.parent;
if (p.parent == null)
root = l;
else if (p.parent.right == p)
p.parent.right = l;
else p.parent.left = l;
l.right = p;
p.parent = l;
}
}
|
红黑树
红黑树和 AVL 树类似,但不准求所有的递归子树高度差不超过 1,而是保证**从根节点到叶尾的最长路径不超过最短路径的两倍,所以他的最坏运行时间也是$O(\text{log}n)$
它的五个约束条件:
1.节点只能是红色或者黑色
2.根节点必须是黑色
3.所有 NIL$^1$ 节点都是黑色
4.一条路径上不能出现相邻的两个红色节点
5.在任何递归子树内,根节点到叶子节点的所有路径上包含相同数目的黑色节点
【说明1】NIL 指在叶子节点不存在的两个虚拟节点,默认是黑色的。
红黑树 VS AVL树
再插入时, 红黑树和AVL树都能在至多两次旋转内恢复平衡。在删除时由于红黑树只追求大致上的平衡, 因此红黑树能在至多三次旋转内恢复和平;而 AVL 树追求绝对平衡, 至多旋转$O(\text{log}n)$次。
因此,面对频繁的插入和删除,红黑树较为合适;面对低频修改、大量查询时,AVL相对合适。
TreeMap
TreeMap 是按照 Key 的排序结果来组织内部结构的 Map 类集合, 它改变了 Map 类散乱无序的形象。 虽然 TreeMap 没有 ConcurrentHashMap 和 HashMap 普及(毕竟插入和删除的效率远没有后两者高),但是在 Key 有排序要求的场景下, 使用 TreeMap 可以事半功倍。
在 TrreMap 的接口继承树, 有两个接口:SortedMap 和 NavigableMap。SortedMap 接口表示它的 Key 是有序不可重复的, 支持获取头尾 Key-Value 元素, 或者根据 Key 指定范围获取子集合。插入的 Key 必须实现 Comparable 或提供额外的比较器 Comparator ,所以 Key 不能是 null ,但是 Value 可以;
NavigableMap 接口继承了 SortedMap ,根据指定的搜索条件返回最匹配的 Key-Value 元素。 不同于 HashMap ,TreeMap 并非一定要覆写 hashCode() 和 equals() 方法来达到Key去重的目的。
关于 TreeMap 和 HashMap 的例子请看《码处高效》P191-P192 ,这里不多做赘述。
类名与属性
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| public class TreeMap<K,V> extends AbstractMap<K,V>
implements NavigableMap<K,V>, Cloneable,java.io.Serializable{
private final Comparator<? super K> Comparator;
private transient Entry<K,V> root;
private static final boolean RED = false;
private static final boolean BLACK = true;
static final class Entry<K,V> implements Map.Entry<K,V> {
K key;
V value;
Entry<K,V> left;
Entry<K,V> right;
Entry<K,V> parent;
}
}
|
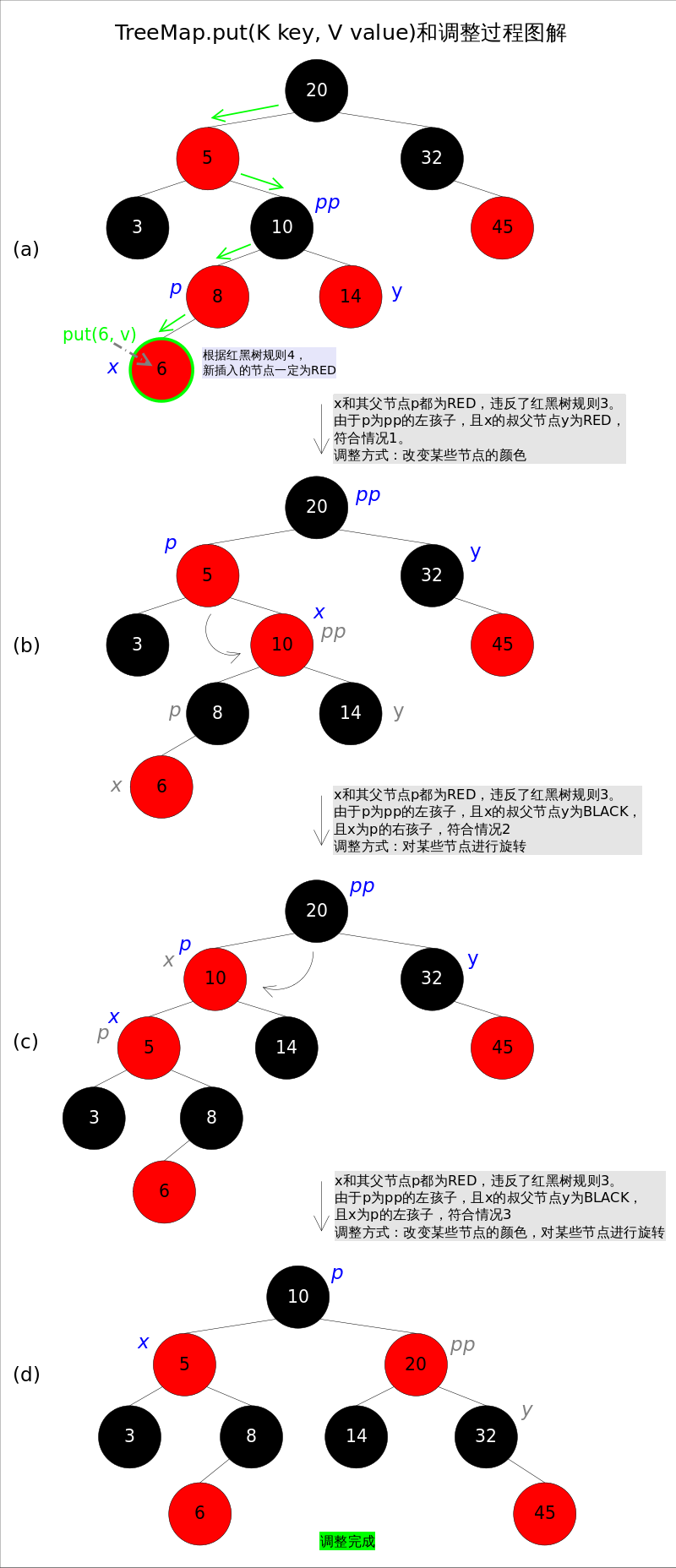
TreeMap 通过 put() 和 deleteEntry() 实现红黑树的增加和删除节点操作,下面的源码分析以插入主流程为例。
再插入新节点之前,要明确三个前提条件:
- 需要调整的新节点总是红色的。
- 如果插入新节点的父节点是黑的,无需调整,因为依然能符合红黑树的5个约束条件。
- 如果插入新节点的父节点是红色的,因为红黑树规定不能出现相邻的两个红色节点,所以进入循环判断,或重新着色,或左右旋转,最终达到红黑树的五个约束条件,退出条件如下:
1
| while(x != null && x != root && x.parent.color == RED)
|
put 源码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
| public V put(K key, V value) {
Entry<K,V> t = root;
if (t == null) {
compare(key, key);
root = new Entry<K,V>(key, value, null);
size = 1;
modCount++;
return null;
}
int cmp;
Entry<K,V> parent;
Comparator<? super K> cpr = comparator ;
if (cpr != null) {
do {
parent = t;
cmp = cpr.compare(key, t. key);
if (cmp < 0)
t = t. left;
else if (cmp > 0)
t = t. right;
else
return t.setValue(value);
} while (t != null);
}
else {
if (key == null)
throw new NullPointerException();
Comparable<? super K> k = (Comparable<? super K>) key;
do {
parent = t;
cmp = k.compareTo(t. key);
if (cmp < 0)
t = t. left;
else if (cmp > 0)
t = t. right;
else
return t.setValue(value);
} while (t != null);
}
Entry<K,V> e = new Entry<K,V>(key, value, parent);
if (cmp < 0)
parent. left = e;
else
parent. right = e;
fixAfterInsertion(e);
size++;
modCount++;
return null;
}
|
重点:fixAfterInsertion() 源码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
|
private void fixAfterInsertion(Entry<K,V> x) {
x. color = RED;
while (x != null && x != root && x. parent.color == RED) {
if (parentOf(x) == leftOf(parentOf (parentOf(x)))) {
Entry<K,V> y = rightOf(parentOf (parentOf(x)));
if (colorOf(y) == RED) {
setColor(parentOf (x), BLACK);
setColor(y, BLACK);
setColor(parentOf (parentOf(x)), RED);
x = parentOf(parentOf (x));
} else {
if (x == rightOf( parentOf(x))) {
x = parentOf(x);
rotateLeft(x);
}
setColor(parentOf (x), BLACK);
setColor(parentOf (parentOf(x)), RED);
rotateRight( parentOf(parentOf (x)));
}
} else {
Entry<K,V> y = leftOf(parentOf (parentOf(x)));
if (colorOf(y) == RED) {
setColor(parentOf (x), BLACK);
setColor(y, BLACK);
setColor(parentOf (parentOf(x)), RED);
x = parentOf(parentOf (x));
} else {
if (x == leftOf( parentOf(x))) {
x = parentOf(x);
rotateRight(x);
}
setColor(parentOf (x), BLACK);
setColor(parentOf (parentOf(x)), RED);
rotateLeft( parentOf(parentOf (x)));
}
}
}
root.color = BLACK;
}
|
这里只展开说一下左旋:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
private void rotateLeft(Entry<K,V> p) {
if (p != null) {
Entry<K,V> r = p. right;
p. right = r.left ;
if (r.left != null)
r. left.parent = p;
r. parent = p.parent ;
if (p.parent == null)
root = r;
else if (p.parent. left == p)
p. parent.left = r;
else
p. parent.right = r;
r. left = p;
p. parent = r;
}
}
|
调整图示
具体例子请看《码出高效》P197-P199
更多数据结构
请访问我的博客-数据结构分类