牛刀小试——买卖一次

买卖股票是 Leetcode 上一系列问题，基本都是用动态规划和贪心算法思想计算出来的。我们看第一个入门级的：

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。设计一个算法来计算你所能获取的最大利润。

示例 1:

1
2
3
4
输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
     注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。

示例 2:

1
2
3
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

分析

我们完全可以用暴力法解决问题，但是有没有一种更好的方法呢？答案是肯定的，我们完全可以一次遍历，只需要两个变量，一个变量存储目前遇到的最小值，一个变量储存目前遇到的最大利润。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public int maxProfit(int[] prices) {
        int min = Integer.MAX_VALUE;
        int max = 0;
        for(int i = 0; i < prices.length; ++i){
            if(prices[i] < min)
                min = prices[i];
            else if(prices[i] - min > max)
                max = prices[i] - min;
        }
        return max;
    }
}

山雨欲来——多次买卖

这次再上一个问题的基础上，改动为了可以多次买卖。

示例 1:

1
2
3
4
输入: [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
     随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。

示例 2:

1
2
3
4
5
输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
     注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。
     因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

分析

我们可以把利润 profit 设为一个累积量，只要下一次的比上一次的大，就把差值累计给 profit ，如果下一次的比上一次的小，更新 min（可以理解为：当n < n-1时，在 n-1 时刻将股票抛售， 在 n 时刻买）
、

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int maxProfit(int[] prices) {
        if(prices.length == 0)
            return 0;
        int min = prices[0];
        int profit = 0;
        for(int i = 1; i <prices.length; ++i){
            if(prices[i] < prices[i-1])
                min = prices[i];
            else
                profit = profit + prices[i] - prices[i-1];
        }

        return profit;
    }
}

风起云涌——只能买两次

示例 1:

1
2
3
4
输入: [3,3,5,0,0,3,1,4]
输出: 6
解释: 在第 4 天（股票价格 = 0）的时候买入，在第 6 天（股票价格 = 3）的时候卖出，这笔交易所能获得利润 = 3-0 = 3 。
     随后，在第 7 天（股票价格 = 1）的时候买入，在第 8 天 （股票价格 = 4）的时候卖出，这笔交易所能获得利润 = 4-1 = 3 。

示例 2:

1
2
3
4
5
输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。   
     注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。   
     因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

分析

这道题有一个常人很容易陷入的误区，一开始我觉得这道题挺简单的，后来发现自己想的有问题,
我一开始的做法是，维护两个最大值，max1,max2，像上面那道题一样，只要下一次的比上一次的大，就把差值累计给 profit ，并和max1、max2对比，如果比其中任何一个大，替换掉那一个，如果下一次的比上一次的小，更新 min，重新计算 profit，但是这样有个问题，加入数组是这样的：

1
[1,2,4,2,5,7,2,4,9,0]

我的方法是,
1->4

1
max1 = 3, max2 = 0;

2->7更新

1
max1 = 5,max2 = 3;

2->9

1
max1 = 7,max1 = 5;

所以我的最终答案是12，然而，最优方法是1->7,2->9此时，最大利润是13.

那么，我们究竟如何取舍呢？

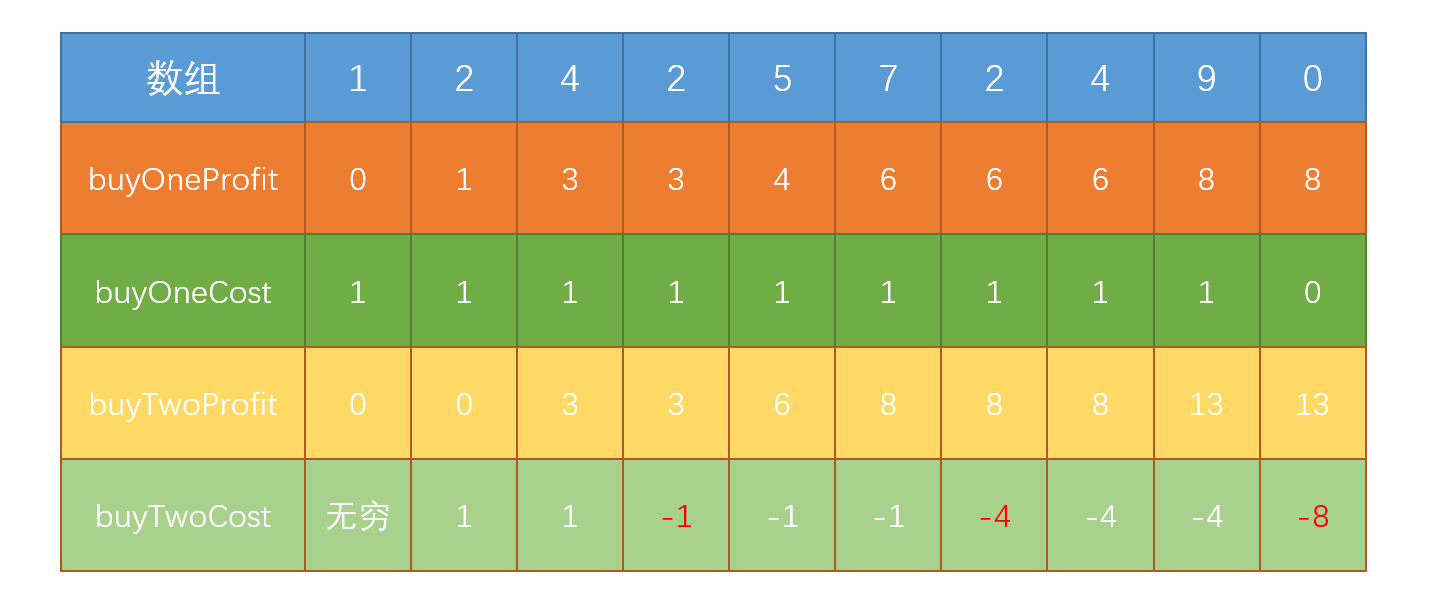
方法一——四变量

其实在第二道题的基础上稍微修改一下思路就好，但不是很容易想到，首先我们要建立一个变量来存储第二次买股票时所花费的费用，这个变量存在的目的意义是为了计算第二次卖出股票时的利润
$$buyTwoProfit = prices[i] - buyTwoCost$$
而这个buyTwoCost至关重要，我们如何确定他的更新呢？其实仔细想想就知道；

  • 首先，第二次买入一定是股票下降的时候
  • 第二次买入一定是赚，确保赚的比之前的第二次买入多才会更新

$$buyTwoCost = prices[i] - buyOneProfit$$

对应代码：

1
buyTwoCost = Math.min(buyTwoCost, prices[i] - buyOneProfit);
四变量过程
四变量过程

方法二——分界线

我们可以换个角度想

最多允许两次不相交的交易，也就意味着这两次交易间存在某一分界线，考虑到可只交易一次，也可交易零次，故分界线的变化范围为第一天至最后一天，只需考虑分界线两边各自的最大利润，最后选出利润和最大的即可。这种方法抽象之后则为首先将[1,n] 拆分为[1,i] 和[i+1,n], 参考卖股票系列的第一题计算各自区间内的最大利润即可。[1,i] 区间的最大利润很好算，但是如何计算[i+1,n] 区间的最大利润值呢？难道需要重复n 次才能得到？注意到区间的右侧n 是个不变值，我们从[1, i] 计算最大利润是更新波谷的值，那么我们可否逆序计算最大利润呢？这时候就需要更新记录波峰的值了

方法一代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public int maxProfit(int[] prices) {
        if (prices == null || prices.length == 0) {
            return 0;
        }
        int buyOneCost = prices[0];
        int buyOneProfit = 0;
        int buyTwoCost = Integer.MAX_VALUE;
        int buyTwoProfit = 0;

        for (int i = 1; i < prices.length; i ++) {
            buyOneProfit = Math.max(buyOneProfit, prices[i] - buyOneCost);
            buyOneCost = Math.min(buyOneCost, prices[i]);
            buyTwoProfit = Math.max(buyTwoProfit, prices[i] - buyTwoCost);
            buyTwoCost = Math.min(buyTwoCost, prices[i] - buyOneProfit);
        }

        return Math.max(buyOneProfit, buyTwoProfit);
    }

方法二代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public int maxProfit(int[] prices) {
    if (prices == null || prices.length <= 1) return 0;
    // get profit in the front of prices
    int[] profitFront = new int[prices.length];
    profitFront[0] = 0;
    for (int i = 1, valley = prices[0]; i < prices.length; i++) {
        profitFront[i] = Math.max(profitFront[i - 1], prices[i] - valley);
        valley = Math.min(valley, prices[i]);
    }
    // get profit in the back of prices, (i, n)
    int[] profitBack = new int[prices.length];
    profitBack[prices.length - 1] = 0;
    for (int i = prices.length - 2, peak = prices[prices.length - 1]; i >= 0; i--) {
        profitBack[i] = Math.max(profitBack[i + 1], peak - p
        rices[i]);
        peak = Math.max(peak, prices[i]);
    }
    // add the profit front and back
    int profit = 0;
    for (int i = 0; i < prices.length; i++) {
        profit = Math.max(profit, profitFront[i] + profitBack[i]);
    }
    return profit;
}

惊涛骇浪——k次交易

示例 1:

1
2
3
输入: [2,4,1], k = 2
输出: 2
解释: 在第 1 天 (股票价格 = 2) 的时候买入，在第 2 天 (股票价格 = 4) 的时候卖出，这笔交易所能获得利润 = 4-2 = 2 。

示例 2:

1
2
3
4
输入: [3,2,6,5,0,3], k = 2
输出: 7
解释: 在第 2 天 (股票价格 = 2) 的时候买入，在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。
     随后，在第 5 天 (股票价格 = 0) 的时候买入，在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。

分析

我们仍然使用动态规划来完成。我们维护两种量，一个是当前到达第i天可以最多进行 j 次交易，最好的利润是多少（global[i][j] ），另一个是当前到达第i天，最多可进行j次交易，并且最后一次交易在当天卖出的最好的利润是多少（local[i][j] ）。下面我们来看递推式，全局的比较简单，global[i][j]=max(local[i][j],global[i-1][j]) ，也就是去当前局部最好的，和过往全局最好的中大的那个（因为最后一次交易如果包含当前天一定在局部最好的里面，否则一定在过往全局最优的里面）。全局（到达第i天进行j次交易的最大收益）= max{局部（在第i天交易后，恰好满足j次交易），全局（到达第i-1天时已经满足j次交易）}对于局部变量的维护，递推式是
$$local[i][j] = max(global[i-1][j-1] + \text{max}(diff,0),local[i-1][j] + diff)$$

也就是看两个量

  • 第一个是全局到 i-1 天进行 j-1 次交易，然后加上今天的交易，如果今天是赚钱的话（也就是前面只要 j-1 次交易，最后一次交易取当前天）
  • 第二个量则是取 local 第 i-1 天j次交易，然后加上今天的差值（这里因为local[i-1][j] 比如包含第i-1天卖出的交易，所以现在变成第i天卖出，并不会增加交易次数，而且这里无论diff是不是大于0都一定要加上，因为否则就不满足local[i][j]必须在最后一天卖出的条件了）。

局部（在第i天交易后，总共交易了j次）= max{情况2，情况1}
情况1：在第i-1天时，恰好已经交易了j次（local[i-1][j] ），那么如果i-1天到i天再交易一次：即在第i-1天买入，第i天卖出（diff），则这不并不会增加交易次数！【例如我在第一天买入，第二天卖出；然后第二天又买入，第三天再卖出的行为和第一天买入，第三天卖出的效果是一样的，其实只进行了一次交易！因为有连续性】
情况2：第i-1天后，共交易了 j-1 次（global[i-1][j-1] ），因此为了满足“第 i天过后共进行了 j次交易，且第i天必须进行交易”的条件：我们可以选择:

  • 在第i-1天买入，然后再第i天卖出（diff）
  • 在第i天买入，然后同样在第i天卖出（收益为0）。

上面的算法中对于天数需要一次扫描，而每次要对交易次数进行递推式求解，所以时间复杂度是$O(n*k)$，如果是最多进行两次交易，那么复杂度还是$O(n)$。空间上只需要维护当天数据皆可以，所以是$O(k)$，当 k=2，则是$O(1)$。
补充：这道题还有一个陷阱，就是当k大于 n（天数）/2 时，其实就退化成第二个问题了

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
public int maxProfit(int k, int[] prices) {
    if (prices == null || prices.length < 2) {
        return 0;
    }
    int days = prices.length;
    if (days/2 <= k) {
        return maxProfit2(prices);
    }
    // local[i][j] 表示前i天，至多进行j次交易，第i天必须sell的最大获益
    int[][] local = new int[days][k + 1];
    // global[i][j] 表示前i天，至多进行j次交易，第i天可以不sell的最大获益
    int[][] global = new int[days][k + 1];
    for (int i = 1; i < days; i++) {
        int diff = prices[i] - prices[i - 1];
        for (int j = 1; j <= k; j++) {
            local[i][j] = Math.max(global[i - 1][j-1]
                        + Math.max(diff, 0),local[i - 1][j] + diff);
            global[i][j] = Math.max(global[i - 1][j], local[i][j]);
        }
    }
    return global[days - 1][k];
}
public int maxProfit2(int[] prices) {
    int maxProfit = 0;
    for (int i = 1; i < prices.length; i++) {
        if (prices[i] > prices[i-1]) {
            maxProfit += prices[i] - prices[i-1];
        }
    }
    return maxProfit;
}