题目

给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。

【举例】
输入: coins = [1, 2, 5], amount = 11
输出: 3
解释: 11 = 5 + 5 + 1

分析

我们仍采取上次说的回溯转动态规划，来慢慢熟悉动态规划解题思路。

回溯

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
public int minCoins(int[] coins, int amount){
    if(coins == null || coins.length == 0 || amount < 1){
        return -1;
    }
    return proress(coins, 0, amount);
}

/**
 * 
 * @param coins coin数组
 * @param i 当前考虑的第i个面值coin
 * @param rest 目前剩下需要换的钱
 * @return 
 */
public int proress(int[] coins, int i, int rest) {
    // base case:
    // 此时已经没有面值能考虑的
    // 所以如果剩下的rest此时不是0，则返回-1
    if(i == coins.length){
        return rest == 0 ? 0 : -1;
    }
    // 最少张数，初始为-1
    int res = -1;
    // 依次尝试使用当前面值(coins[i])0张、1张，但不能超过rest
    for(int k = 0; k * coins[i] <= rest; k++){
        // 使用了k张coins[i]，剩下的钱为rest-k*coins[i]
        int next = proress(coins, i +1, rest - k* coins[i]);
        if(next != -1){
            if(res == -1)
                res = next + k;
            else
                res = Math.min(res, next + k);
        }
    }
    return res;
}

动态规划

  1. 找可变参数，如果看了回溯的代码，马上能确定分别是：硬币面值coins[i]、剩下的钱rest。

  2. 构建表，二维数组的行代表硬币面值，列代表兑换面值，如下图所示。注意，为了构建base case，我们必须要创建0硬币面值，以及0兑换钱数，因为我把0面值放在了数组最后，所以我们运算方向是自下向上的
    二维数组

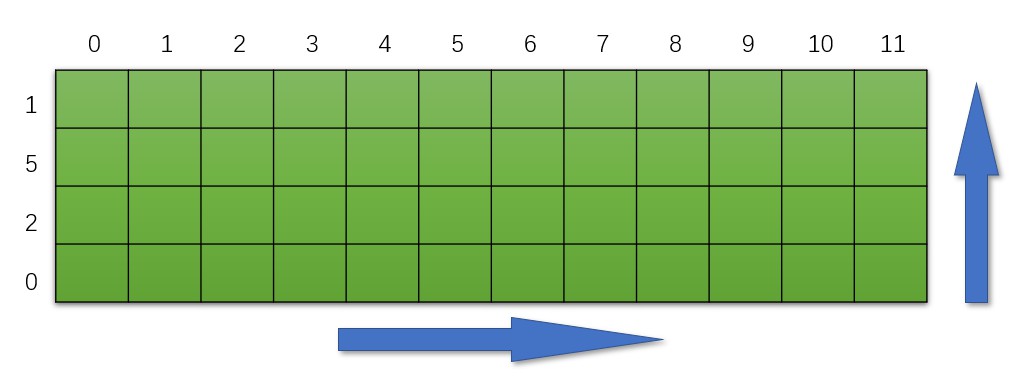
  3. 随后我们对base case进行初始赋值，当0面值时。只有当兑换钱总数为0，数量才是0，其他都是-1(不可达)

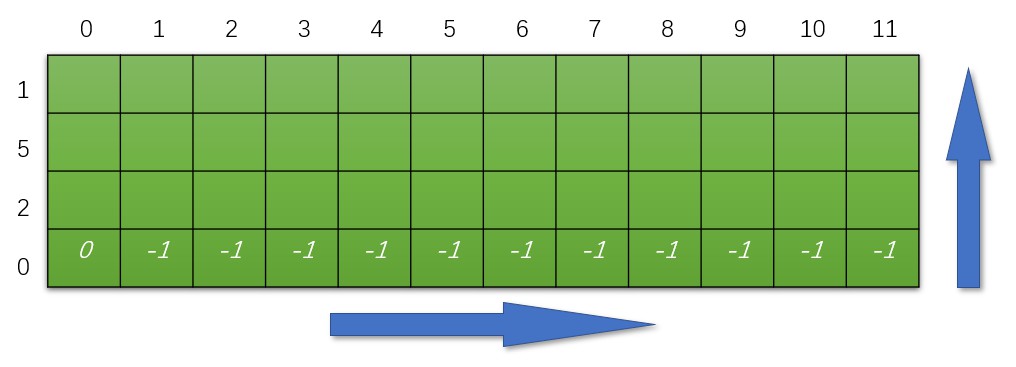
    base case

  4. 最为关键的一步，如何填写非base case，我们要梳理清楚逻辑关系，首先赋值-1，然后我们考虑此时的coin[i]能否构成，不能构成（coin[i] > rest）我们肯定不可达，如果coins[i] < rest ，这是就要看 rest - coins[i] 是否可达，如果不可达，那rest也不可达，如果可达，我们就要和之前没有coins[i]参与的面值组成的rest比一比，谁更小。

以上这段文字需要细细品味，如果你觉得想起来有点吃力，请看下面两张图：

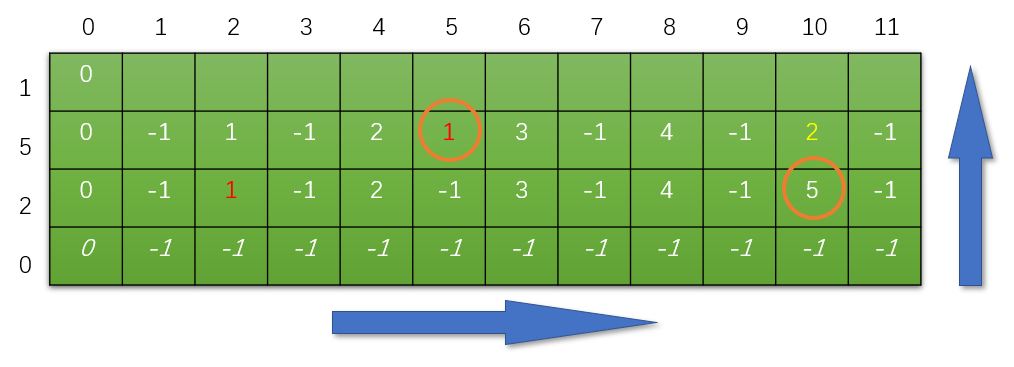
注意红字得到的过程
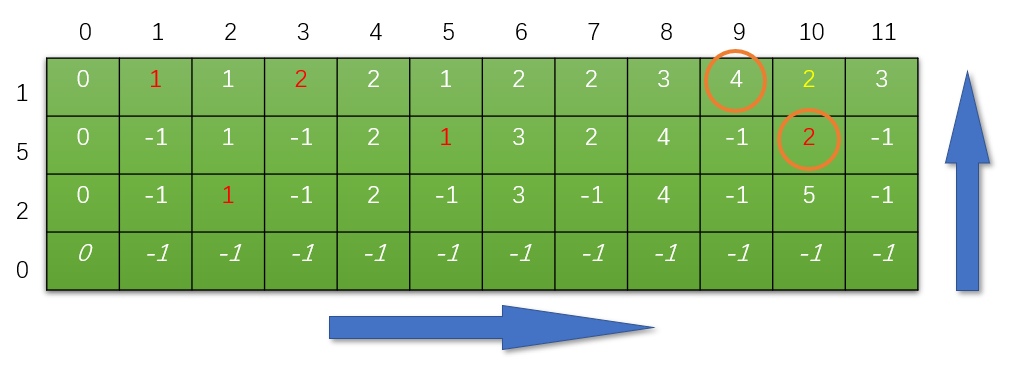
注意红字得到的过程
黄字在图中标出了比较过程
黄字在图中标出了比较过程

这两张图中，我希望你搞清楚红色数字的来由，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
public int minCoins(int[] coins, int amount){
    if(coins == null || coins.length == 0 || amount < 1){
        return -1;
    }
    int N = coins.length;
    int[][] dp = new int[N + 1][amount + 1];
    // base case初始化
    for(int col = 1; col <= amount; col++){
        dp[N][col] = -1;
    }
    for(int i = N - 1; i >= 0; i--){
        for(int rest = 0; rest <= amount; rest++){
            dp[i][rest] = -1;
            if(dp[i + 1][rest] != -1)
                dp[i][rest] = dp[i + 1][rest];
            if(rest - coins[i] >= 0 && dp[i][rest - coins[i]] != -1){
                if(dp[i][rest] == -1)
                    dp[i][rest] = dp[i][rest - coins[i]] + 1;
                else
                    dp[i][rest] = Math.min(dp[i][rest - coins[i]] + 1, dp[i][rest]);
            }
        }
    }
    return dp[0][amount];
}

最后，欢迎大家来我的公众号看一看，周更一些算法总结和Java基础巩固~

微信关注安知窝
微信关注安知窝