S&C算法
S&C 算法是 Schimidl&Cox 同步算法的简称,是一种基于训练序列的同步估计算法,它是由 Schimidl 和 Cox 提出的。它是最经典的一种基于训练序列的同步估计算法,后续的 Minn 算法和 Park 算法都在它基础上做改进的。 S&C 算法的训练序列的结构图如图 3-2 所示。
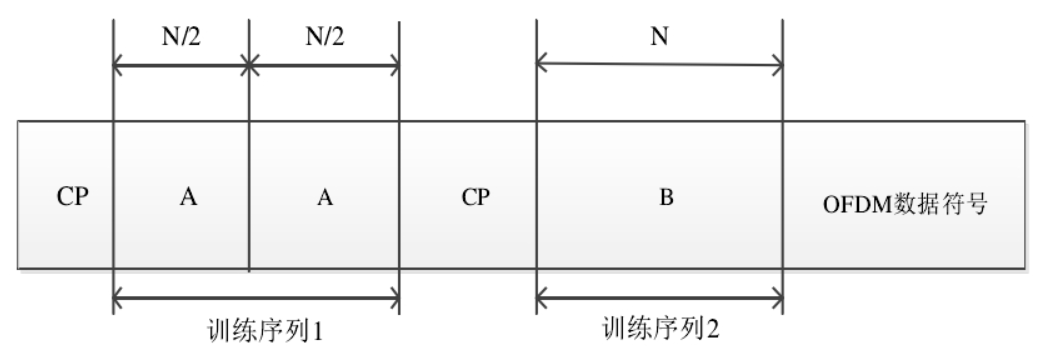
如图 3-2 所示,训练序列 1 由两个长度为 N/ 2 训练序列 A 组成,这两个 A 是完全一样的序列;训练序列 2 由长度为 N 的训练序列 B 组成。训练序列 1 通常是用来完成符号定时估计和小数倍载波偏移估计。训练序列 1 的 N 个子载波的频域特性表现为,在偶数子载波上放置一个长度为 N/ 2 的1PN 序列,在奇数子载波上全部置零,然后进行 N 点的 IFFT 变换,就能够创造出前后 N/2 个点值一样的训练序列 1。具体实现的时候,可以使用 N/2 个点的 PN 序列,进行 IFFT 之后,得到序列 A,把 A 重复放置一次就能得到训练序列 1。训练序列 2 通常是和训练序列 1一起来完成整数倍载波偏移估计的。训练序列 2 的 N 个子载波的频域特性表现为,在奇数子载波上放置一个长度为 N/ 2 的其他序列,在偶数子载波上放置一个长度为 N/ 2 的2PN 序列,然后进行 N 点的 IFFT 变换,就可以得到训练序列 2,其中,2PN 序列与1PN 序列的有一个差分关系,如下式所示,
$v(k)=\frac{P N_{2}(k)}{P N_{1}(k)} \qquad k=1,2, \cdots N / 2$
从训练序列 1 的第一个采样值开始,将前后对应的数据共轭相乘相加,可以得到相关函数,如下式所示:
$P(d)=\sum_{n=0}^{N / 2-1} r^{*}(d+n) r(d+N / 2+n)$
式中 d 表示估计到的滑动窗的起始位置,理想位置就是第一个采样点。峰值会受到 CP 的干扰,进而出现一个平台,我们一般把它称为平台效应。下式表示滑动窗内的信号能量:
$R(d)=\sum_{n=0}^{N / 2-1}|r(d+n+N / 2)|^{2}$
归一化后的定时测度函数可定义为
$M(d)=\frac{|P(d)|^{2}}{R^{2}(d)}$
使得 $M(d)$ 取得最大值的 d 就是估计出的符号起始位置,一般把这个位置记为 $\hat{d}$ ,如下式所示:
$\hat{d}=\arg \max (M(d))$
Minn 算法
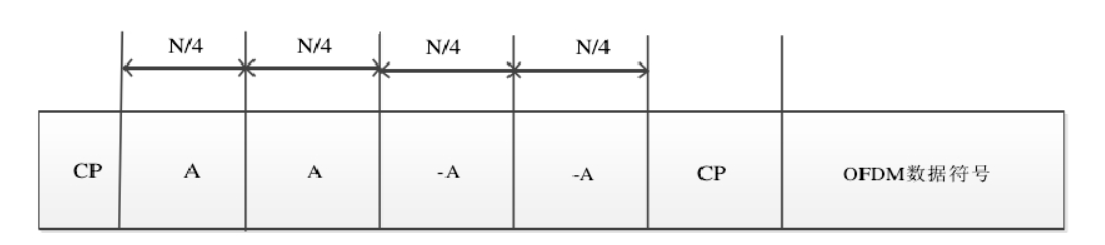
从图 3-4 中可以看到,Minn 算法由 4 个训练符号构成,第一个和第二个训练符号都是 A,第三个和第四个训练符号都是 -A,其中,A 和 -A 互为相反数,A 是由伪随机 PN 序列进行 IFFT 之后得到的。 Minn 算法的运算过程和 S&C 算法的运算过程基本一致,只是由于训练序列结构的改变,导致了相关函数和能量函数也一起发生了变化,具体变化如下式所示:
$P(d)=\sum_{k=0}^{1} \sum_{m=0}^{N / 4-1} r^{*}\left(d+\frac{N \cdot k}{2}+m\right) \cdot r\left(d+\frac{N \cdot k}{2}+m+\frac{N}{4}\right)$
$R(d)=\sum_{k=0}^{1} \sum_{m=0}^{N / 4-1}\left|r\left(d+\frac{N \cdot k}{2}+m+\frac{N}{4}\right)\right|^{2}$
$M(d)=\frac{|P(d)|^{2}}{R^{2}(d)}$
Park 算法
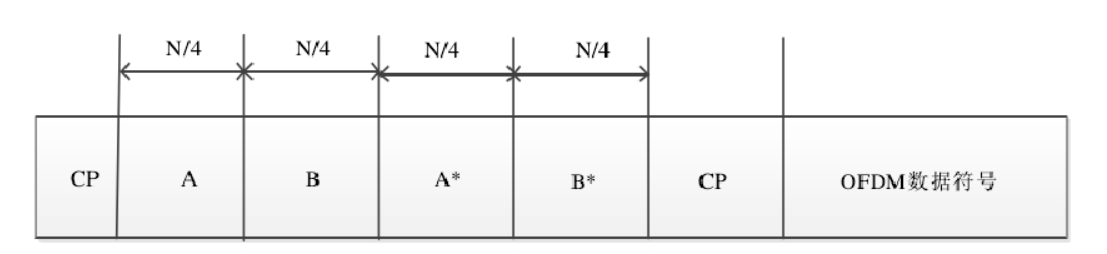
从图 3-5 中可以看出一个 Park 算法的训练序列由四个训练符号构成的。其中 A 是由长度为 N/4 的伪随机 PN 序列经过 IFFT 得到的,B 是 A 的逆向排列,A*是A 的共轭,B*是 B 的共轭。 Park 算法的相关函数,能量函数和定时测度函数定义为:
$P(d)=\sum_{k=0}^{N / 2-1} r(d+k) \cdot r(d-k-1)$
$R(d)=\sum_{k=0}^{N / 2-1}|r(d+k)|^{2}$
$M(d)=\frac{|P(d)|^{2}}{R^{2}(d)}$
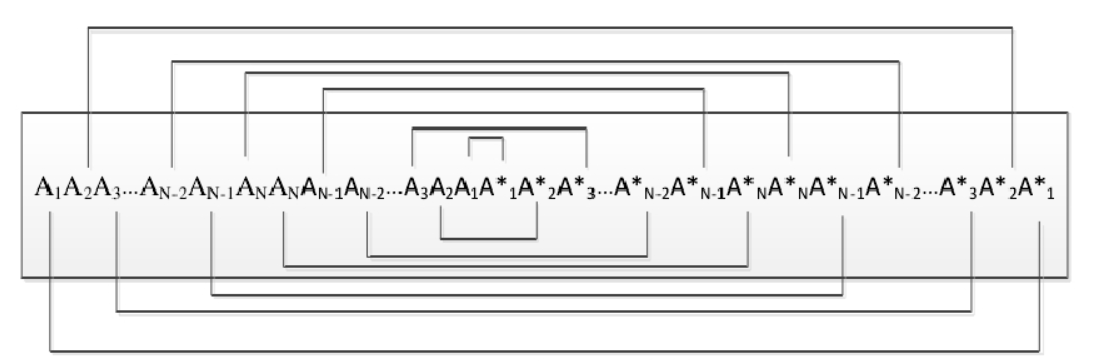
Park 算法的训练序列虽然前后也是对称的,但是并没有利用前后对称这一特性,而是利用了训练序列中心共轭对称这个更难得的性质。从中间两个值向两边依次进行相关运算,才能够达到唯一的相关峰值,排除 CP 的干扰。而且使得归一化后的符号定时测度函数 $M(\hat{d})$ 达到最大的 $\hat{d}$ 对应的并不是 FFT 窗开始的位置,而是训练序列的中点。Park 算法的相关函数的运算过程如图 3-6 所示,
三种算法效果
以上这三种方法在AWGN信道下表现良好
对于 S&C 算法,S&C 算法在各种信道下,在找出理想的 FFT 窗附近都存在着一个“平台”。
对于 Minn 算法和 Park 算法,在 ETU 信道(一种多径干扰模型)下,随着多径衰落、时延和频偏的增加,定时测度函数峰值被削弱,且幅度变化较大,也有可能出现“双峰”的情况,造成定时同步判断的错误。